

The magic and power of calculus ultimately rests on the amazing fact that differentiation and integration are mutually inverse operations. And, just as complex functions enjoy remarkable differentiability properties not shared by their real counterparts, so the sublime beauty of complex integration goes far beyond its real progenitor. Peter J. Oliver
Example \(\PageIndex<1>\) Let’s evaluate \(\int_f\left ( \bar \right )dz\), where \(C\) is given by \(x=3t\), \(y=t^\), \(y=t^\), with \(−1≤t≤4\). Here we have that \(C\) is \(z\left ( t \right )=3t+it^\). Therefore, with the identification \(f\left ( z \right )=\bar\) we have \(f\left ( z\left ( t \right ) \right )=\overline<3t+it^>=3t-it^\). Also, \(z′(t)=3+2it\), and so the integral is \(\int_\bardz=\int_^\left ( 3t-it^ \right )\left ( 3+2it \right )dt\\=\int_^\left ( 2t^+9t+3t^i \right )dt\\=\int_^\left ( 2t^+9t \right )dt+i\int_^3t^dt\\=\left.\left ( \frac<1> t^+\fract^\right )\right|_^+\left.it^ \right |_^\\=195+65i\).
Example \(\PageIndex<2>\) Now let’s evaluate \(\int_^<>\fracdz\), where \(C\) is the circle \(x=cos\,t\), \(y=sin\,t\), with \(0\leq t\leq 2\pi \). In this case \(C\) is \(z\left ( t \right )=cos\,t+i\,sin\,t=e^\), \(f\left ( z\left ( t \right ) \right )=\frac
You can also change the domain coloring plotting option. Drag the points around and observe carefully what happens. Then solve Exercise 1 below.
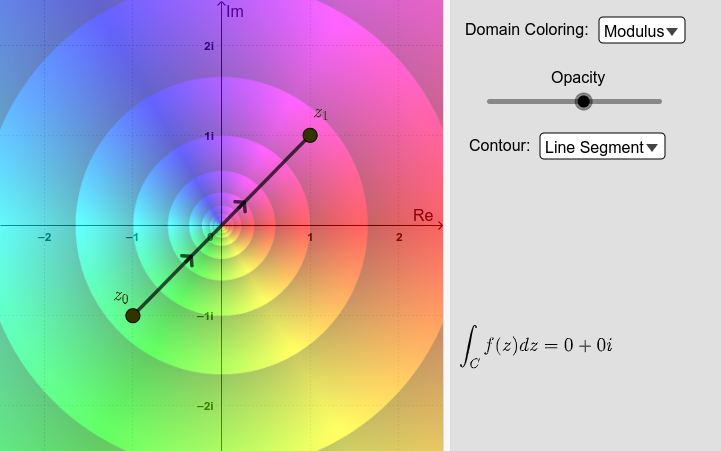
The arrows on the contours indicate direction.
Exercise 1: Use definition (1) to evaluate \(\int_\bardz\), for the following contours \(C\) from \(z_=-2i\) to \(z_=2i\):
Use the applet to confirm your results.
What conclusions (if any) can you draw about the function \(\bar\) from this?
Now use the applet below to explore numerically the integrals
with different contours \(C\) (line segments, semicircles, and circles). Drag the points around and observe carefully what happens. You can select the functions z^2+z or 1/z^2 from the list at the left-top corner. Then solve Exercises 2 and 3.
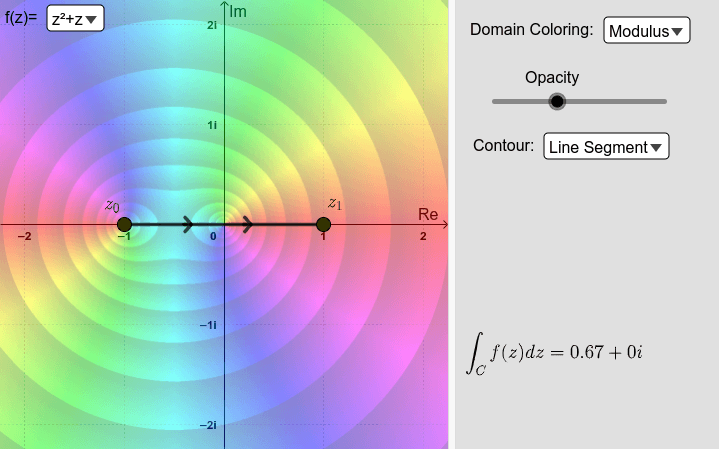
Exercise 2: Consider the integral
Use the applet to analize the value of \(I_\) in the following cases:
What conclusions (if any) can you draw about the value of \(I_\) and the function \(z^+z\) from this?
Exercise 3: Now considering integral
First, in the applet select the function f(z)=1/z^2 . Then analize the values of \(I_\) in the following cases:
What conclusions (if any) can you draw about the value of \(I_\) and the function \(\frac
Although the value of a contour integral of a function \(f(z)\) from a fixed point \(z_\) to a fixed point \(z_\) depends, in general, on the path that is taken, there are certain functions whose integrals from \(z_\) to \(z_\) have values that are independent of path, as you have seen in Exercises 2 and 3. These examples also illustrate the fact that the values of integrals around closed paths are sometimes, but not always, zero. The next theorem is useful in determining when integration is independent of path and, moreover, when an integral around a closed path has value zero. This is known as the complex version of the Fundamental Theorem of Calculus.
Let \(f(z)=F′(z)\) be the derivative of a single-valued complex function \(F(z)\) defined on a domain \(\Omega \subset \mathbb\). Let \(C\) be any countour lying entirely in \(\Omega\) with initial point \(z_\) and final point \(z_\). Then
\(\int_^<>f\left ( z \right )dz=\left.F\left ( z \right ) \right |_>^>=F\left ( z_ \right )-F\left ( z_ \right )\).
Proof: This follows from definition (1) and the chain rule. That is
This page titled 4.2: Complex Integration is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by Juan Carlos Ponce Campuzano.